MESIN TURING
Mesin Turing adalah model komputasi teoretis yang ditemukan oleh Alan Turing, berfungsi sebagai model ideal untuk melakukan perhitungan matematis. Walaupun model ideal ini diperkenalkan sebelum komputer nyata dibangun, model ini tetap diterima kalangan ilmu komputer sebagai model komputer yang sesuai untuk menentukan apakah suatu fungsi dapat selesaikan oleh komputer atau tidak (menentukan computable function). Mesin Turing terkenal dengan ungkapan " Apapun yang bisa dilakukan oleh Mesin Turing pasti bisa dilakukan oleh komputer."
Sebuah mesin turing terdiri atas barisan sel tersusun berupa pita yang dapat bergerak maju mundur, komponen aktif baca/tulis pita yang memiliki status perhitungan serta dapat mengubah/menulisi sel aktif yang ada di pita tadi, dan suatu kumpulan instruksi bagaimana komponen baca/tulis ini harus melakukan modifikasi terhadap sel aktif pada pita, serta bagaimana menggerakkan pita tersebut. Pada setiap langkah dalam komputasi, mesin ini akan dapat mengubah isi dari sel yang aktif, mengubah status dari komponen baca/tulis, dan mengubah posisi pita ke kiri atau ke kanan.
Sejarah Mesin Turing
Jauh sebelum lahirnya program komputer, Alan Turing pada tahun 1936 telah mengeluarkan gagasannya berupa model mesin abstrak sebagai alat mekanik untuk mengerjakan prosedur yang efektif. Model ini disebut Mesin Turing.
Mesin turing dapat diadaptasi untuk mensimulasi logika dari setiap algoritma oleh karena itu cara kerja mesin turing adalah ekivalen dengan cara kerja komputer sekarang ini dan mesin turing juga ekivalen dengan problema komputasi matematika. Mesin turing tidak ditujukan sebagai teknologi komputasi praktis tetapi lebih sebagai eksperimen pemikiran yang mewakili sebuah mesin komputasi. Mesin turing membantu para ilmuan komputer memahami batas-batas komputasi mekanis.
Sebagai input dari mesin turing adalah kata atau untai atas suatu alfabet T. Mesin turing berhenti dengan keadaan menerima atau menolak untai. Kadang-kadang terjadi pula perulangan atau looping tak terhingga.
Keterangan:
· - Tape: Tempat diletakannya inputan yang berupa kata/untai.
· - Head: membaca dan menulisi sel pita mesin turing, bisa bergerak ke kiri atau ke kanan.
· - Finite StateControl (FSC): otak dari TM, diimplementasikan dari algoritma pengenalan kalimat.
Definisi Mesin Turing
Mesin turing didefinisikan sebagai 7 tuple M={ Q, S, G, S, F, Ь, ∆}
Q: himpunan hingga state,
S: alfabet input,
G: simbol pada pita (meliputi pula blank)
S: state awal, S Î Q
Ь: simbol kosong (blank) (bukan bagian dari S )
∆: fungsi transisi
F: state akhir, F Î Q
Gerakan Mesin Turing
Gerakan mesin turing diwakili oleh fungsi transisi:
∆(qi,a)=(qj,b,X): Mesin kedudukan qi membaca simbol masukan a,
gerakan: mesin berubah ke status qj, menulis b dan posisi baca /tulis bergerak X (berupa R=gerak kekanan atau L=gerak kekiri).
Contoh Gerakan Mesin Turing:
II. Dimiliki mesin turing dengan definisi M ={ Q, S, G, S, F, Ь, ∆}
Q={q1,q2}
S = {a,b}
G = {a,b, Ь }
S={ q1}
F={ q2}
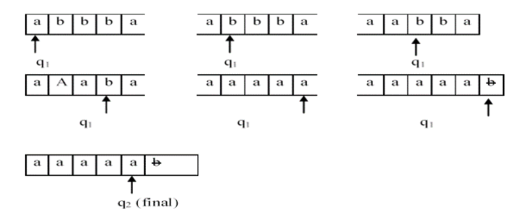
∆: ∆ (q1,a)= (q1,a,R)
∆ (q1,b)= (q1,a,R)
∆ (q1, Ь)= (q2, Ь,L)
Jika di inputkan string “abbba”, maka gerakan mesin turing akan menjadi seperti apa ?
Sebuah contoh mesin Turing dapat dibangun untuk melakukan komputasi sederhana yang didefinsikan seperti ini:
Tentukan ada berapa angka 1 dalam sebuah string berbentuk 0111...110 (rangkaian angka 1 yang didahului dengan 0 dan diakhiri juga dengan 0), apakah berjumlah genap atau berjumlah ganjil.
Jika angka 1 di antara dua angka 0 berjumlah genap, tulis sebuah angka 0 pada salah satu sel dari tape mesin Turing.
Jika angka 1 di antara dua angka 0 berjumlah ganjil, tulis sebuah angka 1 pada salah satu sel dari tape mesin Turing.
Untuk menyelesaikan masalah komputasi ini, kita buat tiga buah State bagi mesin Turing ini, yaitu Start, Even, dan Odd. Di samping itu kita buat sekumpulan aturan Transisi yang digunakan oleh
mesin Turing ini untuk melakukan proses komputasinya. Aturan-aturan Transisi tersebut dapat dituliskan demikian:
-Jika mesin Turing berada pada status Start, dan membaca simbol 0 pada Tape, lakukan hal berikut: Pindah status menjadi status Even, Ganti simbol 0 pada Tape dengan Blank (atau Hapus simbol 0 pada Tape), dan Bergerak ke kanan satu sel.
-Jika mesin Turing berada pada status Even, dan membaca simbol 1 pada Tape, lakukan hal berikut: Pindah status menjadi status Odd, Ganti simbol 1 pada Tape dengan Blank, dan Bergerak ke kanan satu sel.
-Jika mesin Turing berada pada status Odd, dan membaca simbol 1 pada Tape, lakukan hal berikut: Pindah status menjadi Even, Ganti simbol 1 pada Tape dengan Blank, dan Bergerak ke kanan satu sel.
-Jika mesin Turing berada pada status Even, dan membaca simbol 0 pada Tape, lakukan hal berikut: Pindah status menjadi Halt, Ganti simbol 0 pada Tape dengan 0, dan tetap pada sel tersebut (tidak perlu berpindah ke kiri maupun ke kanan).
-Jika mesin Turing berada pada status Odd, dan membaca simbol 0 pada Tape, lakukan hal berikut: Pindah status menjadi Halt, Ganti simbol 0 pada Tape dengan 1, dan tetap pada sel tersebut.
Palindrome itu adalah berasal dari bahasa Yunani yaitu Palindromos A Palindrome. Palindromos A Palindrome adalah kata atau kalimat yang sama dieja maju atau mundur(bacaan yang sama dieja pada kedua arah). Sebagai contoh sederhana adalah beberapa kata yang sederhana yaitu rotor, rotator, civic, madam, racecar, level, dan lain-lain. Untuk contoh lain yaitu kalimat palindrome adalah No lemon no melon, No devil lived on, Swap God for a janitor rot in a jar of dog paws, dll.
Dibawah ini adalah graf dari palindrome detector, merupakan sebuah simulasi mesin turing yang berfungsi untuk mendeteksi kata palindrome yang diinputkan oleh user. Kata atau untai yang dibentuk masih terbatas pada penggunaan huruf “A” dan “B”. Contoh kata yang dibentuk adalah “ABAABBA” untuk kata yang tidak termasuk dalam palindrome, dan “BABBAB” untuk kata yang termasuk dalam palindrome.
Pemrograman sederhana jenis mesin Turing ini tidak sesulit yang dibayangkan. Dimana sebenarnya pemrograman ini akan membentuk graph. Transisi state terdiri dari 5-tupel rangkaian pada setiap baris, dengan format seperti ini:
[state],[karakter],[state baru],[karakterbaru],[arah]
1, _, 2, #, >
2, A, 3, A, >
Karakter '_' dapat digunakan untuk menunjukkan kosong(blank), 'H' untuk menunjukkan sebagai state berhenti/Halt (hanya berlaku pada sisi kanan transisi), dan '<' dan '>' untuk menunjukkan arah masing-masing bergerak kekiri atau kanan.
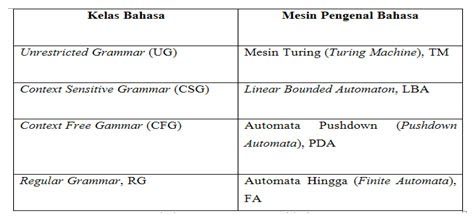
LINIER BOUNDED AUTOMATA
Tetapi kita dapat membatasi kekuatan Mesin Turing dengan cara berikut:
- Jika kita menggunakan TAPE sebagai STACK maka itu akan menjadi "PDA"
- Jika kita membuat TAPE terbatas, maka itu akan menjadi "Finite Automata"
- Jika ukuran TAPE sama dengan ukuran input maka itu akan menjadi "LBA"
Untuk automata terbatas TAPE akan memiliki ukuran tetap terlepas dari ukuran input, sedangkan untuk LBA, ukuran TAPE akan bervariasi: untuk ukuran input lebih besar, TAPE lebih besar dan untuk ukuran input lebih kecil, ukuran TAPE lebih kecil.
Kekuatan LBA
LBA lebih kuat dari PDA misalnya: a n b n c n | n ≥1
tidak dapat diterima oleh PDA sedangkan itu dapat diterima oleh LBA tanpa menggunakan spasi tambahan atau simbol BLANK.
tidak dapat diterima oleh PDA sedangkan itu dapat diterima oleh LBA tanpa menggunakan spasi tambahan atau simbol BLANK.
Pendekatan
Misalkan input adalah: "aaabbbccc"
Tandai 'a' sebagai 'X' dan bergerak ke kanan, tandai 'b' sebagai 'X' dan bergerak ke kanan, tandai 'c' sebagai 'X' dan bergerak ke kiri. Dan ulangi proses ini sampai semua simbol ditandai sama.
Misalkan input adalah: "aaabbbccc"
Tandai 'a' sebagai 'X' dan bergerak ke kanan, tandai 'b' sebagai 'X' dan bergerak ke kanan, tandai 'c' sebagai 'X' dan bergerak ke kiri. Dan ulangi proses ini sampai semua simbol ditandai sama.
Jadi sampai sekarang kita telah melihat semua mesin di bawah ini:
| Nama mesin | Status Setara Deterministik dan Non-Deterministik |
|---|---|
| Automata terbatas | Iya |
| PDA | TIDAK, PDA Non-Deterministik lebih kuat |
| Automata Terikat Linier | Tidak dapat ditentukan |
| Mesin Turing | Iya |
Contoh Standar LBA
Berikut ini adalah contoh standar dari LBA yang perlu diingat
- L = {a n b n c n | n ≥1}
- L = {a n! | n ≥ 0}
- L = {a n | n = m 2 , m ≥ 1}, berarti n adalah kuadrat sempurna
- L = {a n | n adalah prima}
- L = {a n | n bukan bilangan prima}
- L = {ww | w ε {a, b} + }
- L = {w n | w ε {a, b} + , n ≥ 1}
- L = {www R | w ε {a, b} + }
Sumber : https://translate.google.com/translate?hl=id&sl=en&u=https://scanftree.com/automata/linear-bounded-automata&prev=search

 dimana
dimana
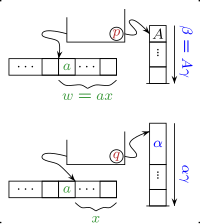

 dimana
dimana

Push Down Automata
Pushdown automata digunakan dalam teori tentang apa yang dapat dihitung oleh mesin. Mereka lebih mampu daripada mesin negara-terbatas tetapi kurang mampu daripada mesin Turing . Automata pushdown deterministic dapat mengenali semua bahasa bebas konteks deterministik sedangkan bahasa non-deterministik dapat mengenali semua bahasa bebas konteks , dengan yang sebelumnya sering digunakan dalam desain parser .
Istilah "pushdown" mengacu pada fakta bahwa tumpukan dapat dianggap sebagai "didorong ke bawah" seperti dispenser baki di kafetaria, karena operasi tidak pernah bekerja pada elemen selain elemen atas. Sebaliknya, stack stack memungkinkan akses dan operasi pada elemen yang lebih dalam. Stack automata dapat mengenali serangkaian bahasa yang lebih besar daripada automata pushdown. Automaton stack bersarang memungkinkan akses penuh, dan juga memungkinkan nilai yang ditumpuk menjadi seluruh sub-tumpukan daripada hanya simbol terbatas tunggal.

Diagram dari automat pushdown
Mesin keadaan terbatas hanya melihat sinyal input dan kondisi saat ini: ia tidak memiliki tumpukan untuk bekerja dengannya. Ia memilih negara baru, hasil dari mengikuti transisi. Pushdown automaton (PDA) berbeda dari mesin keadaan terbatas dalam dua cara:
- Itu dapat menggunakan bagian atas tumpukan untuk memutuskan transisi mana yang akan diambil.
- Itu dapat memanipulasi tumpukan sebagai bagian dari melakukan transisi.
Automat pushdown membaca string input yang diberikan dari kiri ke kanan. Di setiap langkah, ia memilih transisi dengan mengindeks tabel dengan simbol input, kondisi saat ini, dan simbol di bagian atas tumpukan. Automat pushdown juga dapat memanipulasi tumpukan, sebagai bagian dari melakukan transisi. Manipulasi dapat berupa mendorong simbol tertentu ke bagian atas tumpukan, atau melepaskan bagian atas tumpukan. Otomaton dapat secara alternatif mengabaikan tumpukan, dan membiarkannya apa adanya.
Menyatukan: Diberikan simbol input, kondisi saat ini, dan simbol stack, otomaton dapat mengikuti transisi ke keadaan lain, dan secara opsional memanipulasi (mendorong atau meletupkan) stack.
Jika, dalam setiap situasi, paling banyak satu tindakan transisi seperti itu dimungkinkan, maka otomat disebut deterministic pushdown automaton (DPDA) . Secara umum, jika beberapa tindakan dimungkinkan, maka otomat disebut PDA umum , atau nondeterministik . String input yang diberikan dapat menggerakkan otomat pushdown nondeterministik ke salah satu dari beberapa urutan konfigurasi; jika salah satu dari mereka mengarah ke konfigurasi penerimaan setelah membaca string input lengkap, yang terakhir dikatakan milik bahasa yang diterima oleh automaton .
PDA secara resmi didefinisikan sebagai 7-tuple:
-
adalah seperangkat negara yang terbatas
-
adalah himpunan terbatas yang disebut alfabet input
-
adalah himpunan terbatas yang disebut tumpukan alfabet
-
adalah bagian terbatas dari
, hubungan transisi
-
adalah kondisi awal
-
adalah simbol tumpukan awal
-
adalah himpunan negara penerima
Sebuah elemen  adalah transisi dari
adalah transisi dari  . Ini memiliki makna yang dimaksudkan itu
. Ini memiliki makna yang dimaksudkan itu  , dalam keadaan
, dalam keadaan  , pada input
, pada input  dan dengan
dan dengan  sebagai simbol tumpukan teratas, dapat dibaca
sebagai simbol tumpukan teratas, dapat dibaca  , ubah status menjadi
, ubah status menjadi  , pop
, pop  , menggantinya dengan mendorong
, menggantinya dengan mendorong  . Itu
. Itu  komponen hubungan transisi digunakan untuk memformalkan bahwa PDA dapat membaca surat dari input, atau melanjutkan membiarkan input tidak tersentuh.
komponen hubungan transisi digunakan untuk memformalkan bahwa PDA dapat membaca surat dari input, atau melanjutkan membiarkan input tidak tersentuh.
Dalam banyak teks relasi transisi digantikan oleh formalisasi (setara), di mana
-
adalah fungsi transisi , pemetaan
menjadi himpunan bagian terbatas dari
Sini  berisi semua tindakan yang mungkin dilakukan dalam status
berisi semua tindakan yang mungkin dilakukan dalam status  dengan
dengan  di tumpukan, saat membaca
di tumpukan, saat membaca  pada input. Seseorang menulis misalnya
pada input. Seseorang menulis misalnya  kapan tepatnya
kapan tepatnya  karena
karena  . Perhatikan bahwa terbatas dalam definisi ini sangat penting.
. Perhatikan bahwa terbatas dalam definisi ini sangat penting.
Perhitungan

langkah dari automat pushdown
Untuk memformalkan semantik dari otomat pushdown deskripsi situasi saat ini diperkenalkan. 3-tuple  disebut deskripsi sesaat (ID) dari
disebut deskripsi sesaat (ID) dari  , yang mencakup keadaan saat ini, bagian dari pita input yang belum dibaca, dan isi tumpukan (simbol paling atas ditulis terlebih dahulu). Relasi transisi
, yang mencakup keadaan saat ini, bagian dari pita input yang belum dibaca, dan isi tumpukan (simbol paling atas ditulis terlebih dahulu). Relasi transisi  mendefinisikan langkah-relasi
mendefinisikan langkah-relasi  dari
dari  pada deskripsi instan. Untuk instruksi
pada deskripsi instan. Untuk instruksi  ada langkah
ada langkah  , untuk setiap
, untuk setiap  dan setiap
dan setiap  .
.
Secara umum pushdown automata adalah makna non-deterministik yang dalam deskripsi instan yang diberikan  mungkin ada beberapa langkah yang mungkin. Setiap langkah ini dapat dipilih dalam perhitungan. Dengan definisi di atas pada setiap langkah selalu simbol tunggal (atas tumpukan) muncul, menggantinya dengan simbol sebanyak yang diperlukan. Sebagai akibatnya tidak ada langkah yang didefinisikan ketika tumpukan kosong.
mungkin ada beberapa langkah yang mungkin. Setiap langkah ini dapat dipilih dalam perhitungan. Dengan definisi di atas pada setiap langkah selalu simbol tunggal (atas tumpukan) muncul, menggantinya dengan simbol sebanyak yang diperlukan. Sebagai akibatnya tidak ada langkah yang didefinisikan ketika tumpukan kosong.
Komputasi dari automat pushdown adalah urutan langkah. Perhitungan dimulai pada keadaan awal  dengan simbol tumpukan awal
dengan simbol tumpukan awal  pada tumpukan, dan sebuah string
pada tumpukan, dan sebuah string  pada pita input, dengan demikian dengan deskripsi awal
pada pita input, dengan demikian dengan deskripsi awal  . Ada dua mode penerimaan. Automat pushdown menerima dengan kondisi akhir, yang berarti setelah membaca inputnya robot tersebut mencapai kondisi penerimaan (dalam
. Ada dua mode penerimaan. Automat pushdown menerima dengan kondisi akhir, yang berarti setelah membaca inputnya robot tersebut mencapai kondisi penerimaan (dalam  ), atau menerima dengan tumpukan kosong (
), atau menerima dengan tumpukan kosong (  ), yang berarti setelah membaca inputnya robot mengosongkan tumpukannya. Mode penerimaan pertama menggunakan memori internal (keadaan), yang kedua adalah memori eksternal (tumpukan).
), yang berarti setelah membaca inputnya robot mengosongkan tumpukannya. Mode penerimaan pertama menggunakan memori internal (keadaan), yang kedua adalah memori eksternal (tumpukan).
Secara formal seseorang mendefinisikan
-
dengan
dan
(keadaan akhir)
-
dengan
(tumpukan kosong)
Sini  mewakili penutupan refleksif dan transitif dari relasi langkah
mewakili penutupan refleksif dan transitif dari relasi langkah  artinya sejumlah langkah berurutan (nol, satu atau lebih).
artinya sejumlah langkah berurutan (nol, satu atau lebih).
Untuk setiap otomat pushdown tunggal, kedua bahasa ini tidak perlu memiliki hubungan: keduanya mungkin sama tetapi biasanya tidak demikian. Spesifikasi otomat juga harus mencakup mode penerimaan yang dimaksudkan. Diambil dari semua pushdown automata, kedua kondisi penerimaan menentukan kelompok bahasa yang sama.
Dalil. Untuk setiap otomat pushdown  seseorang dapat membuat otomat pushdown
seseorang dapat membuat otomat pushdown  seperti yang
seperti yang  , dan sebaliknya, untuk setiap automat pushdown
, dan sebaliknya, untuk setiap automat pushdown  seseorang dapat membuat otomat pushdown
seseorang dapat membuat otomat pushdown  seperti yang
seperti yang 
Berikut ini adalah deskripsi formal dari PDA yang mengenali bahasa tersebut  menurut keadaan akhir:
menurut keadaan akhir:

PDA untuk 
(dengan kondisi akhir)
(dengan kondisi akhir)
- menyatakan:
- masukan alfabet:
- tumpukan alfabet:
- mulai keadaan:
- mulai simbol tumpukan: Z
- negara penerima:
Relasi transisi  terdiri dari enam instruksi berikut:
terdiri dari enam instruksi berikut:
-
,
-
,
-
,
-
,
-
, dan
-
.
Dengan kata-kata, dua instruksi pertama mengatakan bahwa dalam keadaan p setiap saat simbol 0 dibaca, satu A didorong ke tumpukan. Mendorong simbol A di atas A lainnya diformalkan sebagai mengganti top A dengan AA (dan juga untuk mendorong simbol A di atas Z ).
Instruksi ketiga dan keempat mengatakan bahwa, setiap saat otomat dapat bergerak dari keadaan p ke keadaan q .
Instruksi kelima mengatakan bahwa dalam keadaan q , untuk setiap simbol Saya membaca, satu A muncul.
Akhirnya, instruksi keenam mengatakan bahwa mesin dapat bergerak dari keadaan q ke keadaan menerima r hanya ketika tumpukan terdiri dari satu Z.
Tampaknya tidak ada representasi yang umum digunakan untuk PDA. Di sini kita menggambarkan instruksinya  oleh tepi dari negara p ke negara q diberi label oleh
oleh tepi dari negara p ke negara q diberi label oleh  (baca a ; ganti A dengan
(baca a ; ganti A dengan  ).
).
Memahami proses perhitungan

menerima perhitungan untuk 0011
Berikut ini menggambarkan bagaimana PDA di atas menghitung pada string input yang berbeda. Subskrip M dari simbol langkah  di sini dihilangkan.
di sini dihilangkan.
- Input string = 0011. Ada berbagai perhitungan, tergantung pada saat perpindahan dari status p ke status q dibuat. Hanya satu yang menerima.
-
Status akhir menerima, tetapi input tidak diterima dengan cara ini karena belum dibaca. -
Tidak ada langkah lebih lanjut yang mungkin.
Menerima perhitungan: berakhir pada keadaan menerima, sementara input lengkap telah dibaca.
-
- Input string = 00111. Sekali lagi ada berbagai perhitungan. Tak satu pun dari ini menerima.
-
Status akhir menerima, tetapi input tidak diterima dengan cara ini karena belum dibaca. -
Tidak ada langkah lebih lanjut yang mungkin. -
Keadaan akhir menerima, tetapi input tidak diterima dengan cara ini karena belum (sepenuhnya) dibaca.
-
PDA dan bahasa bebas konteks
Setiap tata bahasa bebas konteks dapat ditransformasikan menjadi otomat pushdown nondeterministic yang setara. Proses derivasi tata bahasa disimulasikan dengan cara paling kiri. Ketika tata bahasa menulis ulang nonterminal, PDA mengambil nonterminal paling atas dari tumpukannya dan menggantikannya dengan bagian kanan aturan tata bahasa ( perluas ). Di mana tata bahasa menghasilkan simbol terminal, PDA membaca simbol dari input ketika itu adalah simbol paling atas pada tumpukan ( kecocokan ). Dalam arti tumpukan PDA berisi data tata bahasa yang tidak diproses, yang sesuai dengan traversal pre-order dari pohon derivasi.
Secara teknis, diberikan tata bahasa bebas konteks, PDA memiliki keadaan tunggal, 1, dan hubungan transisinya dibangun sebagai berikut.
-
untuk setiap aturan
( luaskan )
-
untuk setiap simbol terminal
( cocok )
PDA menerima dengan tumpukan kosong. Simbol tumpukan awal adalah simbol awal tata bahasa.
Untuk tata bahasa bebas konteks dalam bentuk normal Greibach , mendefinisikan (1, γ) ∈ δ (1, a , A ) untuk setiap aturan tata bahasa A → a γ juga menghasilkan otomat pushdown nondeterministic setara.
Kebalikannya, menemukan tata bahasa untuk PDA yang diberikan, tidak mudah. Caranya adalah dengan mengkode dua status PDA ke dalam nonterminal tata bahasa.
Dalil. Untuk setiap otomat pushdown  seseorang dapat membangun tata bahasa bebas konteks
seseorang dapat membangun tata bahasa bebas konteks  seperti yang
seperti yang  .
.
Bahasa string yang diterima oleh otomat pushdown deterministik disebut bahasa bebas konteks deterministik . Tidak semua bahasa bebas konteks bersifat deterministik. [catatan 1] Sebagai konsekuensinya, DPDA adalah varian yang sangat lemah dari PDA dan tidak ada algoritma untuk mengubah PDA menjadi DPDA yang setara, jika DPDA seperti itu ada.
Otomat terbatas dengan akses ke dua tumpukan adalah perangkat yang lebih kuat, setara dengan kekuatan untuk mesin Turing . Otomat terikat linier adalah perangkat yang lebih kuat daripada otomat pushdown tetapi lebih sedikit daripada mesin Turing.
Generalized pushdown automaton (GPDA)
GPDA adalah PDA yang menulis seluruh string dengan panjang yang diketahui ke stack atau menghapus seluruh string dari stack dalam satu langkah.
GPDA secara resmi didefinisikan sebagai 6-tuple:
dimana  , dan
, dan  didefinisikan dengan cara yang sama seperti PDA.
didefinisikan dengan cara yang sama seperti PDA.
-
:
adalah fungsi transisi.
Aturan perhitungan untuk GPDA adalah sama dengan PDA kecuali bahwa  dan
dan  Sekarang adalah string, bukan simbol.
Sekarang adalah string, bukan simbol.
GPDA dan PDA adalah sama karena jika suatu bahasa dikenali oleh PDA, itu juga diakui oleh GPDA dan sebaliknya.
Seseorang dapat merumuskan bukti analitik untuk kesetaraan GPDA dan PDA menggunakan simulasi berikut:
Membiarkan  menjadi transisi dari GPDA
menjadi transisi dari GPDA
dimana  .
.
Bangun transisi berikut untuk PDA:
-
- Sumber : https://translate.google.com/translate?u=https://en.wikipedia.org/wiki/Pushdown_automaton&hl=id&sl=en&tl=id&client=srp
Finite State Automata
23APR
- Sebuah FSA dibentuk dari lingkaran yang menyatakan state:
• Label pada lingkaran adalah nama state
• Busur menyatakan transisi/ perpindahan
• Label pada busur yaitu symbol input
• Lingkaran yang didahului sebuah busur tanpa label menyatakan state awal
• Lingkaranb ganda menyatakan state akhir/ final.
Jadi sebuah mesin otomata dapat dinyatakan dalam diagram transisi, fungsi transisi dan tabel transisi.Jenis FSA
Ada dua jenis FSA :
Deterministic Finite Automata (DFA) : dari suatu state ada tepat satu state berikutnya untuk setiap simbol masukan yang diterima. Deterministik artinya tertentu/sudah tertentu fungsi transisinya.
Notasi matematis DFA:
• M = nama DFA
• Q = himpunan keadaan DFA
• S = himpunan alfabet
• d = fungsi transisi
• q0 = keadaan awal
• F = keadaan akhir
M = (Q, S, d, q0, F)Contoh : Pengujian untuk menerima bit string dengan banyaknya 0 genap, serta banyaknya 1 genap.
0011 : diterima
10010 : ditolak, karena banyaknya 0 ganjil
Diagram transisi-nya :
DFA nya:
Q = {q0 , q1 , q2 , q3 }
Σ = {0,1}
S = q0
F = { q0}
fungsi transisi adalah:
δ( q0,011)= δ( q2,11) =δ( q3,1)= q2 Ditolak
δ( q0,1010)= δ( q1,010) =δ( q3,10)=δ( q2,0)= q0 Diterima - Non-deterministic Finite Automata (NFA) dari suatu state ada 0, 1 atau lebih state berikutnya untuk setiap simbol masukan yang diterima.
Non-Deterministic Finite Automata:
• Otomata berhingga yang tidak pasti untuk setiap pasangan state input, bisa memiliki 0 (nol) atau lebih pilihan untuk state berikutnya.
• Untuk setiap state tidak selalu tepat ada satu state berikutnya untuk setiap simbol input yang ada.
• Dari suatu state bisa terdapat 0,1 atau lebih busur keluar (transisi)
berlabel simbol input yang sama.
• Untuk NFA harus dicoba semua kemungkinan yang ada sampai
terdapat satu yang mencapai state akhir.
• Suatu string x dinyatakan diterima oleh bahasa NFA, M= (Q, _, d, S, F) bila {x | d (S,x) memuat sebuah state di dalam F}Kedua finite automata di atas mampu mengenali himpunan reguler secara presisi. Dengan demikian kedua finite automata itu dapat mengenali string-string yang ditunjukkan dengan ekspresi reguler secara tepat.DFA dapat menuntun recognizer(pengenal) lebih cepat dibanding NDFA. Namun demikian, DFA berukuran lebih besar dibanding NDFA yang ekivalen dengannya. Lebih mudah membangun NDFA dibanding DFA untuk suatu bahasa, namun lebih mudah mengimplementasikan DFA dibanding NDFA.